本文是一篇工程硕士论文,本模型引入图形处理器(GPU)加速计算技术,在不降低精度的条件下大幅提升计算速度,同时将该非结构模型与 CPU 非结构模型以及结构网格的 GPU 全水动力模型的计算时间进行对比,结果表明该非结构 GPU 模型计算效率较高,相较于 CPU 模型,非结构GPU 模型加速比在 38.4 及以上;相较于结构 GPU 模型,非结构 GPU 模型计算效率能提升 2 倍及以上。
1 绪论
1.1 研究背景与意义
1.1.1 研究背景
近年来,随着世界范围内暴雨、冰雹等极端异常天气的频发,泥石流、洪水等由灾害引发的次生灾害也越来越常见[7]。这些灾害事件对人类生命造成危害,造成的经济损失也很严重,而在这些众多的自然灾害中,洪水的破坏力强大,造成损失严重,影响范围广阔,世界上各国多遭受过洪水灾害的影响[8],其造成的生命财产损失占全球所有自然灾害损失的 20%[9]。
由于洪涝灾害越来越频发,当今世界各国对洪涝灾害都非常重视,据权威部门发布的有关报告,在全世界近 180 个国家发生的数千起重大自然灾害中,洪涝灾害发生的次数远超过其它灾害,造成的影响也很大[10]。我国是全球洪水灾害发生最频繁的国家之一,在我国有超过半数的人口居住在洪泛区,超过 70%的财产(包括私人财产、社会财产等)受到洪水的威胁,洪水每年都能对我国造成重大的影响[11],并随着气候变化的加剧,我国的洪水灾害将进一步加大[12]。中国遭受的灾害中以洪水为例,每年造成的直接经济损失以千亿计[13],据相关数据显示,在 2013-2015 年全国平均每年有 180 座城市遭遇洪涝灾害[9],在过去的几十年里,由于自然气候变化或人类影响,中国经历了许多毁灭性的洪水事件,如:1998 年中国特大洪涝灾害[14],北京“721”事件[15],“411”深圳暴雨事件[16]等。以北京“721”事件为例,这次暴雨强度超过了北京近 61 年来所有降雨,引发的严重的洪水灾害,导致 79 人死亡,最终有数百万人受灾,经济损失上百亿元[17]。
洪水除了对中国造成影响之外,在国际上也是一个重大问题。例如在北美,2005 年由于飓风的袭击,新奥尔良遭受洪水的影响,造成上千人死亡,经济损失达数千亿美元,成为美国历史上造成损失最大的洪涝灾害[18];2013 年 6 月 8 日,加拿大的阿尔伯塔南部由于强降水引发洪水,造成城市内道路封锁,多处地区断电,导致约 3 万余人死亡,总损失估计约超 50 亿加币[19];巴基斯坦在 2010 年的七月中旬到八月中旬,有四个省遭受到洪水的影响,造成 5000 人左右的人员伤亡,2300 多万人受到洪水影响,损失惨重。除此之外,在欧洲如德国、瑞士、斯洛伐克、白俄罗斯、波兰、匈牙利和塞尔维亚等国家都受到暴雨导致的极端洪水的影响;东南亚地区由于气候原因,也容易受到洪水影响[20]。
1.2 国内外研究进展
1.2.1 水动力数值模型研究进展
水动力学模型以空间维度为标准,可以将水动力学模型分为一维、二维和三维水动力学模型[40]。在水动力学模型发展之初,一维水动力学模型在河道水动力模拟中应用广泛,一维水动力学模型将河道中的复杂水体的水流流动,包括对流扩散、垂向流等进行概化分析,并沿水流方向将河道划分若干断面,并在断面上假定流速均匀。一维水动力学模型在小型河道,河网的模拟中发挥出色,但无法模拟大江大河、湖泊水库等区域,由于此类区域有诸如湍流、回流、分层流等水动力现象,同时这些过程影响着区域内水质、环境等因素。所以在模拟此类水体时,需要构建更高维度的二维或三维水动力学模型[41]。
如上文所述,世界各地的极端异常气候事件频发,洪涝灾害问题引起了全世界学者的普遍关注[1,42]。自从 1871 年圣维南方程组提出之后,通过计算流体力学及物理模型实验对水流进行研究成为了研究热点。自 1970 年开始,各类水文模型(SWMM、Wallingford等)被广泛应用于防范洪水灾害,包括城市防洪、流域防洪;也有应用其计算城市排水,用于城市规划和环境生态保护工程。尽管这些水文模型对流域的描述越来越精确[43-45],但由于其简化处理了计算单元内水的移动,从而难以实现洪水淹没范围的模拟[20]。国内外学者主要通过差分法、有限元法、有限体积法等,对洪水演进的数值模型进行研究计算[46],采用水动力学模型计算洪水演进过程,得到特定点的水力要素结果,从而得到相对应的水力学要素信息[47-49]。除了这些方法之外,分布式物理模型能考虑到各水力要素的相互作用,使其成为洪涝灾害过程模拟的良好方法[50]。
在洪水分析模型中,常用的一维水动力学模型包括 ISIS、MIKE11 和 HEC-RAS 等。然而一维模型无法准确描述漫滩洪水以及复杂地形及边界条件下的洪水流动过程,应用范围比较局限[20]。为获得精度更高、更加详细的水力学信息要素,二维水动力学模型便体现其优势。对于二维水动力学模型,国内学者也展开了许多相关研究,宋利祥等[51]应用二维水动力模型计算溃坝溃堤洪水演进过程;王志力等[52]利用非结构化的有限体积方法,建立了二维浅水方程模型,对蓄滞洪区滞洪分洪过程进行模拟计算;冀永鹏等[53]对边界及负水深进行了技术改革,提升了模型精度及静水和谐性,并验证了城市区域洪水流动演变过程;Liang 等[54]对海啸风暴潮传播过程方面的模拟计算,取得了较好的效果。
2 计算区域网格处理
2.1 Gmsh 软件介绍
本文使用 Gmsh 软件对研究区域进行网格划分,Gmsh 是一款自动化网格生成的开源软件,使用 Delaunay 算法可以对一维、二维、三维的几何模型进行优化。软件包括几何处理、网格处理、外部求解、后处理等四个模块,同时操作界面简单、使用方便易于上手,操作界面如图 2-1 所示:
Gmsh 相较于其他划分软件有如下优势[71]:
1)能够快速简单地描述包括一维、二维、三维的几何模型;
2)所描述的几何模型可以通过参数进行表示; 3)有多种算法控制划分单元的大小,可以人工控制;
4)可以在多种平台系统运行;
5)可以直观显示划分后的网格。
2.2 Gmsh 模块介绍
上文介绍 Gmsh 包括:几何处理(Geometry)、网格处理(Mesh)、外部求解(Solver)、后处理(Post-Processing)等四个模块,本节主要针对用于网格划分的几何处理(Geometry)、网格处理(Mesh)进行相关介绍。
2.2.1 几何处理(Geometry)模块
几何处理(Geometry)模块的基本思想很简单,如果想要描述一个二维的几何图形,首先等定义若干边界上的点,通过定义好的点连成边界线,由线再构成面,如果构造三维模型则是再由面构成体,几何图形或几何体构成成功之后,用 Physical 赋予每条边、每个面以及每个体的物理属性,其中每个点、线、面等都有其独特的号码标记,并且可以对其进行旋转、按比例放大缩小、对称转化、删除等操作。
Gmsh 可以用“geo”格式的脚本文件来描述所需要的几何图形或几何体,具体格式(只针对二维几何图形)如下:
Point(pn) = {X, Y, Z, cl}; Point 用于描述点的相关信息,其中 Pn表示点号(由自己设定),XYZ 分别为点的坐标,cl 表示网格的大小(可由自己定义)。
Line(Ln) = {p1, p2}; Line 用于描述线的相关信息,其中 Ln表示线号(由自己设定),p1, p2 为组成线的两个点,点的顺序不同,描述线的方向也不同。
Line Loop(LLn) = { L1, L2, L3, L4 }; Line Loop 用于描述线组成顺序环的相关信息,其中 LLn表示环号(由自己设定),L1, L2, L3, L4 为组成该顺序环的四条线,线的顺序不同,描述顺序环的方向也不同。 Plane Surface(Pn) = { LL1 }; Plane Surface 用于描述顺序环构成面的相关信息,其中 Pn表示面号(由自己设定),LL1为组成该面的顺序环。
Physical Line(PLn) = { L1, L2, L3}; Physical Line 用于赋予线物理属性,其中 PLn表示不同的线物理属性(由自己设定),L1, L2, L3 为该拥有物理属性的线。
Physical Surface(PSn) = { Pn }; Physical Surface 用于赋予面物理属性,其中 PSn表示不同的面物理属性(由自己设定),PSn为该拥有物理属性的面
3 基于 GPU 加速技术的二维非结构水动力数值模型 ................................................ 16
3.1 控制方程 ...................................... 16
3.2 数值计算方法 ......................................... 17
4 模型验证及洪水演进过程数值模拟研究 ....................................... 26
4.1 全溃坝水流算例 .................................. 26
4.1.1 模型计算条件 ................................... 26
4.1.2 计算结果对比分析 ........................................... 26
5 结论与展望 ................................................ 52
5.1 结论 ....................................... 52
5.2 展望 ............................................... 53
4 模型验证及洪水演进过程数值模拟研究
4.1 全溃坝水流算例
此算例基于 Stoker 于 1957 年推导出的一维瞬时全溃坝水流的解析解,用于检验数学模型的精度。
4.1.1 模型计算条件
本算例基于 Stoker 推导的解析解,故设定情况均为理想情况。设定一段河渠,河渠长为 1000 m,宽为 100 m,以左下角为坐标原点,坝体位于 x= 500 m 处;河道不设坡度与阻力;边界除下游外均为固壁边界,下游为自由出流边界,同时忽略大坝的厚度;生成的 msh 文件共 2632 个计算网格,1427 个节点,网格平均面积约为 38 m2,网格示意图如下所示。
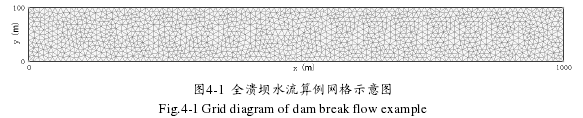
4.1.2 计算结果对比分析
根据下游河床初始水深是否大于 0,该算例分为两种情况,当为 t= 0 s 时,开始瞬时溃坝:
1)下游河床初始水深大于 0
考虑了下游河床初始水深大于 0 的情形,即以大坝为分界线,大坝上游水位为 5 m,大坝下游水位为 0.2 m,初始流速为 0。
文章模拟计算了 60 秒的溃坝洪水演进过程,每隔 10 秒输出一个结果文件,克朗数取0.8。将不同时刻,即 t = 10,20,30,40,50,60 s 时,模拟结果的水位、流速结果与理论解析解对比,对比结果如图 4-2 与图 4-3 所示,模拟结果与解析解吻合度较高。
2)下游河床初始水深等于 0
考虑了下游河床初始水深等于 0 m 的情形,即以大坝为分界线,大坝上游水位为 5 m,大坝下游水位为 0 m,初始流速为 0 m/s。
5 结论与展望
5.1 结论
随着全球气候变化的大背景下,由极端异常天气引发的诸如洪水等灾害也日益频繁,造成的人民生命财产损失也更加严重。为了响应国家对于洪水灾害的政策,配合建设洪水风险图的编制,使用水动力数值模型是一个重要的技术手段,有助于发挥防洪减灾的功能,可以增加防洪减灾的效益。本文以开发一套对地形描述更加精确,模拟精度更高,计算速度更快的水动力数值模型为目标,使用非结构网格划分为基础,通过求解平面二维浅水方程(SWE)来模拟雨水汇流及洪水演进过程,同时 GPU 对计算过程进行加速计算,开发了一套基于 GPU 加速的二维非结构水动力数值模型。
该模型网格使用非结构网格,针对地表水数值模拟会遇到复杂计算区域以及不规则地形等,相较于结构网格,其生成更加的简单,对复杂构型强大的灵活性可以适应各种复杂地形,减少了不必要的网格数目,可以有效应用于各类复杂地形及边界条件。洪水演进过程采用 Godunov 格式的有限体积法数值求解二维浅水方程,同时引入图形处理器(GPU)加速计算技术,建立了一个基于 GPU 技术和非结构网格求解的二维水动力数值模型。
通过模拟计算五个经典算例,包括全溃坝水流算例、混合流算例、三角形挡水建筑物算例、具有干湿界面的静水算例、三驼峰溃坝波算例,验证了模型计算的准确性、和谐性、水量守恒、稳定性等,表明了模型可以良好处理复杂混合流态、拥有高分辨率激波捕获能力。另外通过模拟计算实际洪水演进过程,包括 Toce 河实验算例、Malpasset 溃坝算例。模拟结果表明,该模型可有效应用于实际洪水演进过程模拟,包括普通洪水演进过程、洪水漫滩过程,溃坝等,洪水到达特定点的时间误差较小,模拟结果与文献值、实测值吻合度较高。通过上述算例表明,该模型能很好地模拟洪水演进,可以适应各类复杂地形及边界条件、可按照需求获得特定点的详细水力要素结果以及拥有较高的计算效率等特点。
参考文献(略)
