本文是一篇计算机论文,本文选用粗粒度异步微流水线设计方法研究、设计多模式矩阵加速器,提出内-外积混合算法、稀疏矩阵存储方案,最后基于110𝑛𝑚制程在ASIC前端设计流程下实现支持多种低阶张量计算的多模式矩阵加速器,完成仿真、验证。
第一章绪论
1.1研究背景和意义
张量代数(Tensor Algebra)是向量、矩阵和高阶张量间的计算,普遍存在于数值计算[1]。通常,高阶张量间的运算通过将高阶张量分解为低阶张量(即,矩阵、向量)间的运算来完成。低阶张量运算在机器学习[2-3]、图神经网络[4-5]、线性代数求解器[6-7]、环境分析[8-9]等众多应用领域中扮演重要角色,因其丰富的应用场景受到国内外学者广泛的关注。
矩阵乘法、矩阵向量乘法是张量代数中两个常见的计算。现代科学与工程应用中的矩阵通常是不规则、稀疏的,如计算物理问题中由相对较少的微分项导出的矩阵、深度学习训练过程中的输入矩阵等。因此,稀疏矩阵乘法(General SparseMatrix-Matrix Multiplication,SpGEMM)、稀疏矩阵向量乘法(Sparse Matrix-VectorMultiplication,SpMV)作为两个重要的计算基础,在现代科学与工程应用中占据大量计算时间。
稀疏矩阵的稀疏度高、规模大以及元素分布不规则等特征给计算架构提出三大挑战:(1)高效访问稀疏矩阵中的非零元素;(2)减少对中间结果操作;(3)格式化结果并写回内存中。高稀疏度是指矩阵中的非零元素远小于矩阵的维度积。早在20世纪60年代,研究者们就已发现在计算机使用二维数组处理稀疏矩阵十分低效。2003年,OSKI库[10]形式化稀疏矩阵表示方案,并确定许多优化方案,为稀疏代数的专用软件库奠定基础。然而,中央处理器(Central ProcessingUnit,CPU)内存吞吐率瓶颈使得软件实现的单核性能具有欺骗性,通常只达到峰值性能的10%[11]。图形处理器(Graphics Processing Unit,GPU)在稀疏矩阵向量乘法和稠密矩阵乘法上表现出令人满意的计算效率,但是稀疏矩阵乘法情况则更加复杂。在计算的过程中,在任何位置都可能出现非零元素,需要复杂内存管理和负载均衡[12]。尽管GPU的峰值理论吞吐量超过4𝑇𝐹𝐿𝑂𝑃𝑆,但是当矩阵稀疏度降至0.1%以下时,计算单元明显未得到充分利用,实际性能通常达到低于1𝐺𝐹𝐿𝑂𝑃𝑆[13]。
1.2国内外研究现状
近年来,众多加速稀疏矩阵乘法、稀疏矩阵向量乘法的硬件加速器被国内外研究者们提出。针对不同的应用领域,不同的专用硬件加速器在矩阵算法、存储结构和系统架构等方面创新优化,采用硬件描述语言(Hardware DescriptionLanguage,HDL)实现,最终在FPGA或ASIC上实现加速稀疏矩阵乘法、稀疏矩阵向量乘法。设计专用硬件加速器,解决CPU在相关应用领域中的算力不足问题,弥补GPU在面向高稀疏度的矩阵乘计算时效率低问题。
1.2.1矩阵乘加速器研究现状
2016年谷歌推出第一代TPU[20](Tensor Processing Unit),主要要用于模型的推理(inference)。从第二代TPU开始到2024年发布的第六代TPU[21],TPU的核心用途已经转到AI的模型训练。脉动阵列是TPU的核心部件,其规模从256×256到改进到128×128,有效提高脉动阵列的利用率[22-24]。
Subhankar Pal等人于2018年提出基于外积算法的OuterSPACE[13]。它由单程序多数据(Single Program Multiple Data,SPMD)的处理单元,分布式内存,高速crossbar型总线以及高带宽存储(High Bandwidth Memory,HBM)构成。其中,单程序多数据处理单元通过二级缓存从主存中获取数据。
2020年,Zhekai Zhang等提出SpArch[25],该加速器通过对输入矩阵进行压缩减少中间结果数量,将矩阵乘外积算法中的乘法和合并阶段流水线化提升性能,行预取器(row prefetcher)改善因矩阵压缩导致矩阵𝐵取数速度的降低,霍夫曼树结构的调度器降低内存拥塞。Eric Qin等人提出面向DNN训练中不规则、非结构化的稀疏矩阵乘法的SIGMA[26],采用bitmap格式记录稀疏矩阵中的非零元素的位置信息,设计前向加法网络(Forwarding Adder Network,FAN)用于部分结果累加。Nitish Srivastava等人提出的MatRaptor[27],首次探索基于Gustavson算法的稀疏矩阵加速器,并提出硬件友好的C2SR存储格式。
第二章相关技术原理
2.1矩阵乘算法
1858年,英国数学家阿瑟·凯莱(Arthur Cayley)发表的《矩阵论的研究报告》,打开了矩阵计算的大门。矩阵乘作为矩阵论中的基本运算之一,在众多领域应用广泛。时至今日,已有多种矩阵乘算法被提出。根据它们的算法特征,将其应用在不同的地方。给定矩阵𝐴∈𝑅𝑚×𝑛,矩阵𝐵∈𝑅𝑛×𝑝,矩阵A和矩阵B相乘结果为矩阵𝐶∈𝑅𝑚×𝑝,用于描述此节的矩阵算法。本节介绍5种常见的矩阵乘算法。
2.1.1内积算法
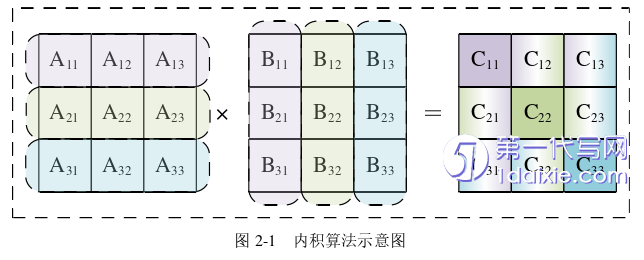
内积(Inner Product)作为最常见的矩阵乘算法。结果矩阵𝐶由矩阵A中的每行逐次乘以矩阵𝐵中的每列得到,即𝐶𝑖,𝑗=𝑎𝑖·𝑏𝑗,其中𝑎𝑖为矩阵A中的第𝑖行,𝑏𝑗为矩阵𝐵中第𝑗列。考虑如果每次只能计算长度为𝑛的向量点乘的情况。对于𝑚行的矩阵𝐴,需要访问𝑚次矩阵𝐵,故内积算法的输入复用性较差。每次的行列点乘运算,都可以得到结果矩阵𝐶中的1个元素值,因此外积算法的输出复用性较好。当𝑚=𝑛=𝑝=3时,内积算法如图2-1所示。
2.2稀疏矩阵存储格式
一般矩阵存储方案(即,二维数组)存储稀疏矩阵是低效且高功耗的,因为大部分的内存被用来存储零值元素,且零值元素参与运算。通过采用稀疏矩阵存储格式,提高存储的利用效率。假设稀疏矩阵𝐴∈𝑅𝑚×𝑛,记非零元素个数为𝑁,用于此节存储空间的分析。本节将介绍COO、CSR、BCSR、ELL、DIA和HYB六种常见的稀疏矩阵存储格式。
2.2.1 COO存储格式
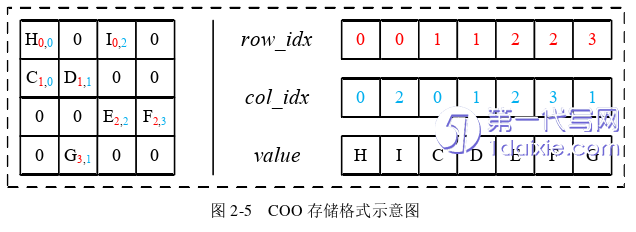
COO存储格式(Coordinate)[44]由三元组(𝑟𝑜𝑤_𝑖𝑑𝑥,𝑐𝑜𝑙_𝑖𝑑𝑥,𝑣𝑎𝑙𝑢𝑒)构成,三元组的长度等于非零元素的个数。其中,𝑣𝑎𝑙𝑢𝑒存储稀疏矩阵中的非零元素,𝑟𝑜𝑤_𝑖𝑑𝑥,𝑐𝑜𝑙_𝑖𝑑𝑥存储非零元素行索引(row index)与列索引(column index)构成的坐标。这是一种最为直观稀疏矩阵的存储方案。存储稀疏矩阵𝐴需要存储空间(𝑠𝑖𝑧𝑒𝑣𝑎𝑙𝑢𝑒+𝑠𝑖𝑧𝑒𝑟𝑜𝑤_𝑖𝑑𝑥+𝑠𝑖𝑧𝑒𝑐𝑜𝑙_𝑖𝑑𝑥)×𝑁,存储关系是Θ(3𝑁)。图2-5为𝑚=𝑛=4下的COO存储格式示意图。
第三章矩阵加速器的存储格式、分块策略与算法分析................22
3.1稀疏矩阵存储格式分析.....................22
3.2矩阵分块策略分析.......................23
第四章异步多模式矩阵加速器架构设计...................33
4.1系统架构.....................33
4.2控制单元(CU_M)与矩阵计算微码.....................34
第五章异步多模式矩阵加速器的实现与验证................................56
5.1异步多模式矩阵加速器测试方案设计.....................56
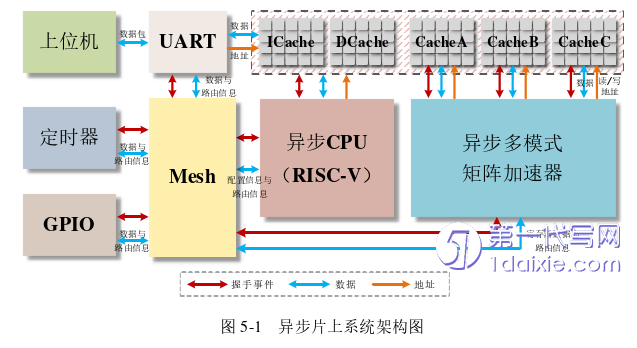
5.1.1异步片上系统整体架构..............................56
5.1.2测试数据集....................................57
第五章异步多模式矩阵加速器的实现与验证
5.1异步多模式矩阵加速器测试方案设计
测试数据集
SciPy是一个用于数学、科学和工程计算的Python开源库,它建立在NumPy之上,提供了许多高效的数值算法和工具,能够帮助研究人员更方便地处理各种科学计算任务。SciPy由多个子模块组成,每个子模块专注于特定的科学计算领域。scipy.sparse及其子模块提供了用于处理稀疏矩阵的工具。
由于目前多模式矩阵加速器中的处理单元仅支持整型数据类型,本研究使用scipy.sparse模块随机生成128×128的矩阵、以及长度为128的向量作为多模式矩阵加速器的整型测试数据集,用于验证多模式矩阵加速器在不同模式下的计算操作是否正确。
图5-2为矩阵、向量的生成代码,通过修改random函数中的函数变量调整生成矩阵和向量的特征。scipy.sparse模块并不支持生成BCSR/BCSC格式压缩的稀疏矩阵,所以random函数中的𝑓𝑜𝑟𝑚𝑎𝑡参数指定为dense生成非压缩格式下的矩阵。通过修改random函数中的𝑑𝑒𝑛𝑠𝑖𝑡𝑦变量来改变生成矩阵、向量的稀疏度。然后调用定制的矩阵、向量格式转换函数CompressVector和CompressMatrix,对源矩阵、源向量和计算结果中的矩阵、向量进行压缩,并写入文件。random函数中的参数𝑚,𝑛用于调整生成矩阵的维度,参数𝑑𝑡𝑦𝑝𝑒用于调整矩阵中元素的数据类型,由于要符合当前版本矩阵加速器的计算特征,在生成随机矩阵、向量的步骤中不做更改。
第六章结论
6.1总结
低阶张量计算是张量代数中的重要部分,如稀疏矩阵乘法、稀疏矩阵向量相乘等计算在图神经网络、线性系统求解等多种科学计算领域扮演重要角色。数据稀疏、数据分布零散等稀疏矩阵特征使得CPU、GPU等计算硬件无法充分发挥其性能优势。专用硬件加速器一般专注于某种计算的优化,无法完整实现实际的算法流程。本文聚焦高能效的多模式矩阵加速器,基于BCSR格式采用粗粒度异步微流水线,提出一种支持11种计算模式的矩阵加速器。最终,本文采用110𝑛𝑚制程完成多模式矩阵加速器的ASIC前端设计流程并进行详细分析。本文的主要工作如下:
(1)粗粒度异步微流水线设计方法的应用,实现无全局时钟。第二章详细介绍粗粒度异步微流水线包含Fifo、分支、融合三种核心结构,和具体的8种模块。本研究借助粗粒度异步微流水线取消时钟数降低整体功耗,同时大大降低异步电路设计难度,将复杂逻辑成功映射成硬件电路。多模式矩阵加速器划分为异步微流水流水线构成的控制通路和大量组合逻辑、寄存器组成的数据通路,脉冲是模块间的通信介质,数据与脉冲的绑定确保整个加速器的正常工作。
(2)提出基于BCSR格式的存储方案,并设计内-外积矩阵乘算法。第三章首先分析2.2节介绍的存储策略,本研究选取BCSR格式存储稀疏矩阵,提高单次计算的并发性。接着统计分析305个稀疏矩阵在常见的分块策略下的平均有效块占比和平均零值填充率,决定采用4×4的分块策略,保证BCSR格式存储效率的同时,和2×2分块策略相比有着4倍的计算性能提升。基于上述的分析结果,针对规模128×128的稀疏矩阵,采用4×4分块策略,在BCSR格式基础上,结合片内存储每行大小128比特的实际情况,创新设计有利于代码库实现的矩阵和向量的存储方案。最后在BCSR格式的基础上,凭借内积算法和外积算法各自的优势,提出一种基于“内积-外积”融合的矩阵乘算法。借助内积算法输出复用性优势,降低生成结果矩阵或向量压缩格式的难度。凭借外积算法所具备的输入复用特性,减少局部取数的频次,增强局部计算效能,以此推动整体计算性能的提升。
参考文献(略)
