本文是一篇计算机论文,本文面向时态图,研究在指定时间区间内通过某顶点的最短环计数问题,兼顾结构因素与时间约束,旨在提出一种高效的查询算法,为时态图分析与应用提供基础支持。
1.绪论
1.1研究背景
随着大数据时代的到来和信息技术的迅猛发展,各行各业的数据量呈指数级增长,而这些海量数据背后蕴藏着不可估量的价值等待着人们发现。为此,数据挖掘、分析技术、数据仓库以及人工智能算法等技术的不断研发和推陈出新,为大规模数据的存储和知识发现提供了丰富的理论基础和技术支撑。
在众多数据结构中[1],图网络模型作为刻画现实世界中不同类型个体及其关系的有效手段,已广泛应用于社交网络[2-4]、通信系统[5-7]、生物网络[8-11]、交通网络[12-13]和电子交易系统[14]等多个关键领域。基于图论和复杂网络的分析方法,研究者得以分析其中个体间的关联性以及揭示网络结构的拓扑特征。这已经成为图挖掘研究的核心内容,从而推动了社区发现[15]、顶点分类[16]、传播机制建模[17]等方向的深入发展。
在图数据分析中,最短环是顶点参与信息回路交互的最小闭合路径,是分析局部交互效率[18-19]、反馈机制及异常模式[20]的重要工具之一。与一般意义上的环结构不同,最短环强调环路长度最小,具有更强的结构代表性和实际意义。其中最短环计数问题,即统计从某个顶点出发所能构成的所有最短环的数量,近年来在金融反欺诈[21-22]、社交行为分析[23-25]、交通调度优化等领域中展现出广泛的应用价值。

1.2研究现状
1.2.1简单图上的最短环计数
本文工作与最短环计数问题相关,学术界对最短环计数问题进行了广泛研究,现有的解决方案通常面向简单非时态图,其核心思想通常通过最短路径计数索引间接实现最短环计数。作为最短环计数的基础,最短路径计数方法发展较为成熟,其主要处理策略是构建基于2-hop的路径计数索引。
Zhang等人[33]提出的HP-SPC算法,首次结合顶点重要性排序构建精确的最短路径覆盖索引,实现了无向图中任意两点最短路径数量的准确计算。其基本流程为:按照重要性降序处理每个顶点,并为每个顶点生成与高等级hub顶点之间的路径标签。然而,该方法索引体积大、构建时间长,在处理大规模图数据时存在空间与时间瓶颈。
为缓解HP-SPC的空间与构建瓶颈,Wang等人[34]提出ST-SPC算法,该算法通过将图分解为稀疏的树部分和密集的核心部分,并为每部分构建不同的索引结构,从而优化了索引空间和构建效率。该方法支持并行索引构建,可以通过增加线程数来加速索引的构建过程。
此外,为解决索引构建中的顶点顺序依赖问题,Peng等人[35]提出PSPC算法,通过并行构建机制实现多线程加速索引构建,显著提高了索引构建效率。Feng等人[36]进一步研究了动态图场景下的最短路径计数问题,提出DSPC算法,仅更新受增删边影响的局部索引,显著提升了动态维护效率。
2.相关定义及算法
2.1相关算法
给定一个简单有向图,现有的最短环计数方法主要可以分为三类:第一为基于直接遍历的搜索方法;第二是将最短环计数问题拆解并转化为多个最短路径计数问题来求解的方法;第三是仅通过一次最短路径计数操作,就能完成最短环计数问题求解。
2.2.1基于直接遍历的搜索方法
该方法主要基于BFS和双向广度优先搜索(Bi-directional Breadth-First Search,BI-BFS)这两种思想。这些方法不需要事先构建索引,但查询速度较慢,尤其在处理大规模图时无法高效响应。
BI-BFS方法:通过同时进行正向和反向BFS搜索,当两个搜索过程相遇时,即可确定经过顶点v的最短环。将相遇的这一层顶点都遍历完后,看得到顶点v的最短环计数。尽管这种方法能在一定程度上减少搜索空间,提高效率,但对于大型图,尤其是在实时更新的场景下,仍然无法快速响应。
2.2问题动机与分析
现有时态图上的简单环路搜索的研究主要聚焦于时序环检测,这类研究侧重于分析环路中边的时间演化过程。然而,在许多应用场景中,例如欺诈检测,更关注的是在给定时间窗口内识别资金是否形成闭环,而非严格要求交易按时间顺序流转。此外,环的数量及其长度在不同时间窗口内的分布同样具有重要意义,有助于揭示潜在的异常交易模式。
假设某银行的反欺诈系统正在监测一名可疑用户q的交易行为。为了判断该用户是否可能涉及欺诈活动,银行希望分析该用户的交易网络,寻找涉及q的资金流动闭环。在分析过程中,以下几个关键因素很关键。首先,欺诈交易通常在短时间内完成,因此银行需要在特定时间窗口内检测环状资金流动。其次,欺诈团伙往往采用最少的交易步数完成资金回流,以减少风险,因此银行更关注最短环的交易路径。最后,若在不同时间窗口内发现大量最短环,说明该用户可能是欺诈网络的核心顶点。因此,银行可以提出一个查询,计算给定多个时间窗口内,通过用户q参与的最短资金环数量及其长度。最短环计数问题与时态环检测不同,它允许环内的交易发生在时间窗口内的任意顺序,只要所有交易均在给定时间范围内即可。这种方法能够更全面地捕捉隐藏的资金回流模式,提高欺诈检测的有效性。目前,关于最短环计数的研究主要集中在简单图上,难以直接应用于时态图。现有方法主要通过索引加速查询来提高效率,但这些方法未充分考虑时间维度的影响,难以应对不同时间窗口下的最短环计数查询。
3.时态图上最短环计数在线查询算法................................19
3.1问题动机与分析................................19
3.2在线算法............................................21
4.基于SCPI索引的时态图上最短环计数查询算法...........................24
4.1问题分析.............................................24
4.2 SCPI索引...........................................25
5.基于ATI索引的时态图中最短环计数查询算法.........................36
5.1问题分析...................................36
5.2 ATI索引...........................................36
6.实验结果与分析
6.2数据集
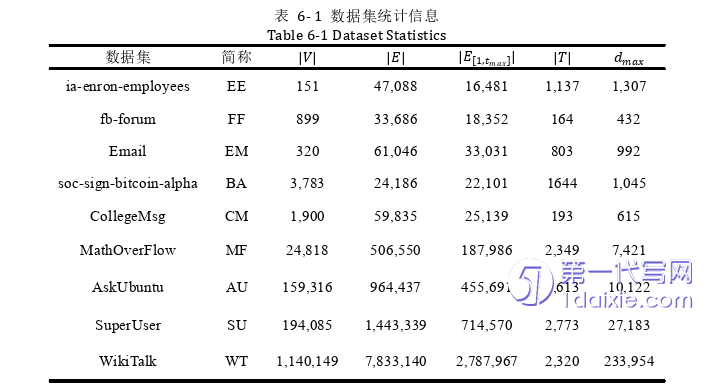
本文选取了9个具有代表性的真实时态有向图数据集进行实验,涵盖了企业通信、社交平台、问答社区等多种交互场景。所有的图都是时态有向图,均不包含自环和重边,相关统计信息如表6-1所示。
这9个数据集分别是:ia-enron-employees、fb-forum、Email、soc-sign-bitcoin-alpha、CollegeMsg、MathOverFlow、AskUbuntu、SuperUser和WikiTalk,其缩写分别为:EE、FF、EM、BA、CM、MF、AU、SU和WT。前两个数据集来自NetRep1:ia-enron-employees是公司内部员工邮件往来的时态图,fb-forum是技术论坛用户互动的时态图;后七个数据集来自SNAP2:Email是发件人与邮件之间的关系时态图,soc-sign-bitcoin-alpha是比特币场外交易平台的信任评价时态图,CollegeMsg是UC-Irvine校园社交平台的用户消息时态图,MathOverFlow是数学问答社区的用户讨论时态图,AskUbuntu是技术问答平台的用户交流时态图,SuperUser表示综合问答网站的互动时态图,以及WikiTalk是维基百科用户协作编辑的通信时态图。
7.结论与展望
7.1研究结论
本文研究了时态图上的最短环计数问题,主要解决如何在给定时间区间内,快速、高效地查询以给定顶点为核心的最短环长度及其计数。本文工作的主要贡献如下:
(1)结合时间窗口设定,明确定义了查询输入、结果要求及约束条件,提出了一种基于朴素BFS思想的在线查询算法,该方法可以适用于任意时间区间与任意顶点的即时查询场景。
(2)为了提升在线查询算法的查询性能,提出了基于索引的高效查询算法的解决方案。此方案分为两种索引支持的查询框架——SCPI索引与ATI索引。SCPI索引维护了图中每个顶点所有最短环长度及其计数发生的有效时间区间,查询效率极高;而ATI索引只维护了图中每个顶点无环状态的有效时间区间,能够有效剪枝无效路径,从而减小了搜索空间,加速了最短环计数的查询。相较在线查询算法,SCPI索引适用于中小规模图,查询效率最好可快4个数量级;ATI索引在大规模数据集上表现优越,查询效率较在线方法提升了3个数量级。
(3)提出了一种针对ATI索引的优化构建算法,利用无环时间的单调性,采用局部更新策略维护无环时间信息,从而避免冗余计算,提高索引构建效率。实验结果表明,优化算法能够高效地完成ATI索引构建,并且在大规模时态图上的构建效率相较于基础构建算法提升了3个数量级,显著缩短了索引构建时间。
参考文献(略)
