本文是数学作业范文的留学生作业范例,题目是“Unexpected Mathematics: Benford's Law and Other Surprising Distributions (意想不到的数学:本福德定律和其他意想不到的分布)”,本福德定律是一个令人惊讶的数学概念,乍一看似乎是反直觉的。它解释了一组大数据中前导数字的分布。一个简单的例子显示了它最初的特性。想象一下,我们看看富时350指数(FTSE 350)上每家公司的当前股价。富时350指数是英国最大的350家公司的指数。在这组数据中,每个股价的第一个数字都有可能是1到9之间的任何数字(d∈{1.…9})。
Introduction引言
Benford’s law is a surprising mathematical concept which at first seems rather counter-intuitive. It explains the distribution of the leading digits in a large set of data. A simple example displays its initial peculiarity. Imagine we look at the current share price of every company on the FTSE 350. an index of the 350 largest UK companies. Within this set of data, each share price has the possibility of the first digit being any number between 1 and 9 ( d∈{1.…9})
The average person would believe that each price would have an equal chance of starting with each number between 1 and 9. so if one of the 350 prices was selected at random the probability that the first digit was 1 would be about 19 (11.1%) and the probability of the first digit being a 9 would also be about 19 (11.1%). However, this is in fact not the case at all. If you were to calculate this, the probability of the first digit being 1 would actually be closer to 30% than 11%. Furthermore, the probability of the leading digit being a 9 would only be just over 4%! I initially read about this strange distribution in an economics context. I was keen to investigate the mathematics behind this and test the limits and applications of it. The physicist Frank Benford first discovered this in 1938 when he noticed that pages closer to the beginning of his log tables were increasingly becoming more worn than those closer to the end, meaning that they were searching for numbers that were starting with a 1 much more than higher numbers. Benford started to test this theory across newspapers, populations and river lengths. He found more or less the same result every single time. Numbers starting with a 1 turned up approximately 30% of the time, almost all the time. Eventually, this was formed into a mathematical law which includes an equation which displays the exact probabilities of each number between 1 and 9 occurring as the leading digit. The aim of this investigation is to explore the explanations and applications behind Benford’s Law and to touch upon other equally strange distributions and examine if they link to Benford’s law in any way. NB: For the purposes of this exploration, all logarithms will be assumed as base 10 if the base is not stated.
Why Study Leading Digits?
Before discussing the law’s explanations and applications, it is first useful to understand how leading digits are studied in the world of mathematics and their importance. Scientific notation (also known as standard form) is a pivotal part of this. The notation follows the system that a positive number x can be expressed in the form S(x)×10n in which 1≤Sx<10. meaning that the number is expressed first as a value of 1 or greater but less than ten, multiplied by 10 to a given exponent which reaches the initial number. For example, in this format the number 865.000.000 would be expressed as 8.65×108 The initial number before the exponent is known as the significand.1 This system allows numbers spanning many different magnitudes to be expressed in a similar fashion, for example comparing atomic radii to planetary radii.
An Overview of the Law
After Benford’s experiments, he discovered the approximate percentages for the probability of each number occurring as the leading digit. The pattern followed in a way as shown on the graph below:
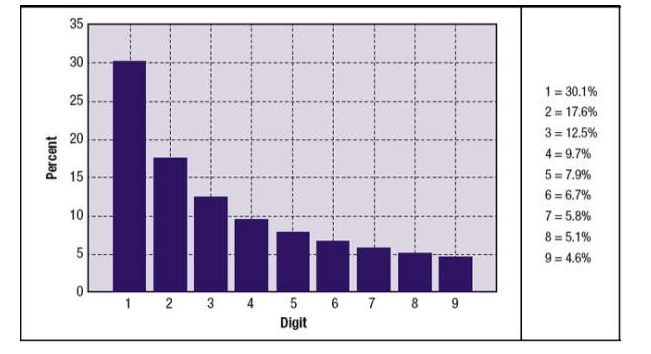
2
For the purposes of explaining the law and the derivation of its equation, the leading digit between 1 and 9 is represented as d with the probability of the digit being the leading digit is represented as P(d).
The basic explanation of the law states that the space between digit d and d+1 is proportional to the quantity of P(d) on a logathrimic scale. A logarithmic scale is one which is non-linear3 and based on orders of magnitude meaning each increasing unit on the scale is the unit on the previous value multiplied with a constant.
Deriving the Equation of the Law推导定律方程
By understanding logathrimic scales we can begin to better understand how the percentages in Benford’s law are derived. When we are working with many values spanning multiple orders of magnitude, as Benford’s law does, the basic explanation states that:
通过理解对数尺度,我们可以更好地理解本福德定律中的百分比是如何推导出来的。当我们处理多个数量级的多个值时,就像本福德定律一样,基本的解释是:
The leading digit d will be 1 when log1≤logd
log2–log1 =0.301
log10–log9 =0.0458

If we apply this to all the numbers between 1 and 9 the results are as follows:
These log calculations are in fact the probabilities of each number from 1 to 9 occurring as the leading digit! This can be seen on the graph of the results below, which follows the exact same pattern as the graph shown above.
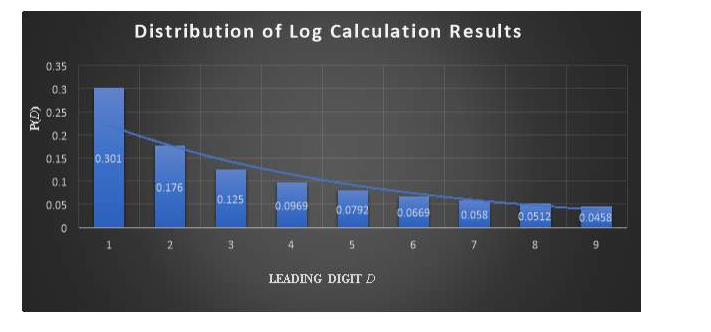
如果我们把这个应用到1到9之间的所有数字,结果如下:
这些对数计算实际上是从1到9的每个数字作为前导数字出现的概率!这可以在下面的结果图中看到,它遵循与上面显示的图完全相同的模式。
From this we can see that the probability P(d) is given by the log of the digit subtracted from the log of the digit plus one i.e:
P(d)=log10d+1–log10d = log10(d+1d)
Further explanations and details of the Law法律的进一步解释和细节
Aside from the initial explanation of the law and the derivation of the equation, there are more detailed explanations and perspectives to the law and how it works. One of these is the Geometric Explanation.1This approach to the law follows the idea that in a model of a number n in a constant growth rate, n will spend a greater amount of time ‘hanging around’ the lower digits than the higher ones. To better explain this, I will refer back to an economically minded example of a geometric series, compound interest. A geometric series is a series in which there is a constant ratio r between each term u and (u+1). 4Therefore the deductive rule follows as Un=U1r n-1. For this compound interest example, let us assume I invest $2000 in 2019 for my retirement in a very generous savings account with an annual 7% interest rate for the long term of 60 years. This function is modelled by the equation Un =2000×1.07n. Note the absence of the subtraction of 1 from n in the exponent. This is due to the fact that we wish to calculate the value as compounding at the end of each year so the subtraction of 1 is not useful. This model shows that the balance in the savings account at the end of the 60 years will be 2000×1.0760=$115.892.85. However, we are more interested in where the balance lies at the end of each year over the whole period rather than just the end. See the appendices for the full balance sheet at the end of each year. When we examine this table from a Benford perspective, we can see that the balance does indeed tend to stay towards low numbers for the first digit and quickly accelerates through the higher numbers. For example, the period between when the balance is $10.000 and $20.000 lasts from 10 years from 2043 to 2053 during which the first digit is 1 on the balance sheet. The table below illustrates this for the point between $10.000 and $99.000 in the account.
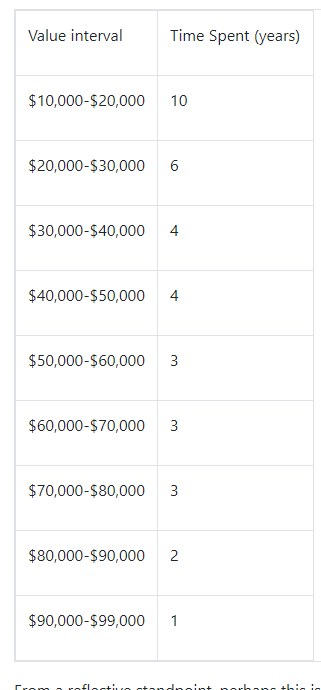
除了最初的法律解释和方程式的推导之外,还有更多关于法律及其工作原理的详细解释和观点。其中之一是几何解释(Geometric explanation)。1这一定律的方法遵循这样的思想:在一个以恒定增长率为基础的数字模型中,n会花更多的时间“徘徊”在较低的数字上,而不是较高的数字上。
From a reflective standpoint, perhaps this is why we as humans focus so heavily on financial achievements which essentially get us ‘back to one’ such as setting targets at one million or one billion. A more recent example of this is Apple making headlines for being the first company to achieve a net worth of $1trillion. Maybe the fact that financially we spend such a long time at these lower values makes them more psychologically valued to us as humans once we reach them at the next order of magnitude.
Scale Invariance尺度不变性
Another aspect of Benford’s Law which adds to its uniqueness is it’s universality. What I mean by this is that if a situation follows Benford’s law, it will tend to continue to follow Benford’s law no matter what operators are imposed upon it. For example, if I took the data set used in the previous explanation, the list of the investment balance year upon year and converted it into every single commonly used currency in the world, from the Euro to the Pound and Vietnamese Dong, the chances are the data would continue to satisfy Benford’s law in almost every single currency. Since each value in the list would have the same operation applied to it, this means it is still likely to span many orders of magnitude which is the main condition for Benford’s Law to apply.
本福德定律的另一个增加其独特性的方面是它的普遍性。我的意思是,如果一种情况遵循本福德定律,那么它将会继续遵循本福德定律,无论什么操作者强加于它。例如,如果我在前面的解释,使用的数据集的列表的投资资产转换成每一年度世界上常用的货币,欧元,英镑和越南盾,有可能数据将继续满足本福德定律几乎在每一个单一货币。
Extensions of the law: Digits beyond the first
Another aspect of Benford’s Law is that it can be extended to further digits rather than just the first digit of the number.5 It is possible to calculate the probability of a number occurring as the 2nd or 3rd digit. To do this we must manipulate the equation into a series in sigma notation which allows us to express a series of additions in one notation. If we have a digit between 0 and 9 (NB: zero can now be included as it is not possible to have zero as the first digit of a number but it is certainly possible to have it as a following digit) then the probability that this digit will be the nth digit in a number is given by the equation:
∑x=10n–210n–1log10(1+110x+d)
In which d represents a number between 0 and 10 and n represents the nth digit which the probability is wanted to be calculated for. However, this is only particularly useful up to the 3rd digit as once the calculation is past the 3rd digit the numbers follow a more expected distribution and tend closer to each number appearing 10% of the time i.e truly random.
Applications of Benford’s Law本福德定律的应用
Benford’s law has one major application which makes it particularly useful, fraud detection. Due to the fact that Benford’s law is present in every aspect of life when numbers are distributed, any large sets of data which do not follow Benford’s Law could be argued to be fraudulent, particularly financial data. Programs which test for compliance with Benford’s Law are often used by tax institutions or banks during audits or to check if data submitted to them is possibly fraudulent. Benford’s Law was also used as part of fraud detection in the 2009 Iranian election6. This raises the question as to if it is moral to use mathematical laws in legal proceedings or as evidence in prosecutions. This morality debate is even more prevalent when there is a certain degree of uncertainty within the law, or limitations to the law as will be discussed below.
本福德定律有一个重要的应用,这使得它特别有用,那就是欺诈检测。由于本福德定律在数字分布时存在于生活的各个方面,任何不遵循本福德定律的大数据集都可能被认为是欺诈的,尤其是金融数据。税务机构或银行在审计或检查提交给他们的数据是否可能存在欺诈时,经常使用测试是否符合本福德法的程序。
Limitations to Benford’s Law本福德定律的局限性
Not every single set of data will be able to follow Benford’s law, for example telephone numbers, human height in meters or feet and page numbers of small documents. Benford’s law also does not apply to data which is generated by humans themselves or written within specific ranges. The chance of Benford’s Law being useful highly depends on how many orders of magnitude the data set spans. For example, the earlier example of human height in meters or feet doesn’t follow the law as it only spans one order of magnitude. In meters almost all human heights will start with a 1. possibly with a few that start with 2 or less than 1. The same applies if human height is measured in feet, there would have to be a human over 3 meters tall in order to exceed the 10ft boundary into the next order of magnitude! Also, if there an extremely large number of orders of magnitudes, then the law also may not apply. For example, Benford’s law wouldn’t apply to the data set of all real numbers, as clearly if these numbers continue to go on forever then then the probability for each digit from 1 to 9 to be the leading digit will be the same.
并不是每一组数据都能遵循本福德定律,例如电话号码、人的身高(米或英尺)和小文件的页码。本福德定律也不适用于由人类自己生成的或在特定范围内编写的数据。本福德定律发挥作用的机会很大程度上取决于数据集能跨越多少数量级。
Further analysis: Similar Laws?
Benford’s law is surprisingly not alone in its strangeness. Contrary to what one may think after reading about the uniqueness of Benford’s law, there are a few other patterns and principles which exist through many different areas of life. Some of these have mathematical patterns which could link to Benford’s law. One of these is Ziph’s Law which relates to language and literature rather than numerical data. Ziph’s Law states that in a large set of words, if the most frequent word is taken, the second most frequent word will appear half as often as the most frequent word and the third most frequent word will appear half as often as the second most frequent word. Essentially, the frequency of a word will be inversely proportional to how often the word appears overall. For example, the most common word in the English language is the word ‘the’ which accounts for 7% of all words appears twice as much as the second most common word ‘of’ which accounts for 3.5% of all words. An equation for Ziph’s law has been created in the context of the English language which states that in a distribution of X number of words in the language, the frequency of each word occurring in relation to its rank of how common it is follows this equation:
1/k∑x=1X1/n
In which X is the number of words in the English language and k is their sequential rank of how common they are in the language. Some have argued that Benford’s law is simply a special case of Ziph’s law however I personally believe they should be held as separate laws. Ziph’s law could better be considered as literature’s version of Benford’s law.
Conclusion结论
Overall, Benford’s Law is deeply rooted into the way numbers are distributed in the real world and it’s useful applications cannot be denied. The law which at first seems strange and unexplainable can indeed be explained and analysed as I have demonstrated throughout this investigative report. The geometric analysis behind Benford’s Law is key to its explanation. Understanding Benford’s Law is now extremely useful as a student deeply interested in the field of economics and finance. I had always been curious into how institutions such as HMRC are able to detect fraud and prosecute those who avoid tax or commit fraudulent actions. Through conducting this exploration, I have been able to gain a greater understanding of mathematics while also being able to explore this economic aspect of fraud detection. Overall, I now have a greater understanding of how mathematics can connect with other fields, even literature which the average person might say is the ‘furthest you can get from mathematics’ is seen to have a mathematical distribution through Ziph’s Law. This exploration continues to demonstrate how mathematics is rooted in every part of life even if we cannot notice it at first.
总的来说,本福德定律深深植根于数字在现实世界中的分布方式,它的有用应用是不可否认的。正如我在整个调查报告中所展示的那样,起初看起来奇怪和无法解释的法律确实可以被解释和分析。本福德定律背后的几何分析是解释它的关键。对于一个对经济和金融领域非常感兴趣的学生来说,理解本福德定律非常有用。
数学作业相关专业范文素材资料,尽在本网,可以随时查阅参考。本站也提供多国留学生课程作业写作指导服务,如有需要可咨询本平台。
